Introduction to statistics and probability

Dr. Huidae Cho

Department of Civil Engineering...New Mexico State University

Contents

1 Statistics vs. probability
2 Inductive vs. deductive reasoning
3 What is the probability of a coin landing on heads?
4 Dice questions
5 Bayes’ theorem
6 Failing in math and/or science
7 Uncertainty
8 Epistemic vs. aleatory uncertainty
9 Probability distribution
10 Central limit theorem demo
11 Statistics
12 Reading materials

1 Statistics vs. probability

Statistics involves the frequency analysis of past events and “enables us to measure the extent to which our world is ideal” (Skiena 2001).

Probability deals with the likelihood of future events and “enables us to find the consequences of a given ideal world” (Skiena 2001).

Edit

2 Inductive vs. deductive reasoning

Inductive reasoning starts with observations and analyzes data to formulate a theory.

Deductive reasoning starts with ideas or premises and observes data to make a conclusion.

Edit

3 What is the probability of a coin landing on heads?

Do you know this probability in advance without any experiments?

Do you have to throw a coin a lot of times to observe what happens?

Edit

4 Dice questions

What is the probability of a die rolling a 1?
What about a 1 and then a 6 in a sequence?
A 1 and a 6 from two dice simultaneously?

Edit

5 Bayes’ theorem

\[P(A|B) = \frac{P(A\cap B)}{P(B)} = \frac{P(B|A)P(A)}{P(B)}\]

Edit

6 Failing in math and/or science

Probability of failing in math: $P(M)=0.3$

Probability of failing in science: $P(S)=0.2$

Are these two events related or independent?

Probability of failing in both math and science: $P(M\cap S)=0.1$

What is the probability of failing in either math or science $P(M\cup S)$?

What is the probability of failing in science when you learned that you failed in math $P(S|M)$?

Edit

7 Uncertainty

We have to embrace uncertainty when studying science because we only have limited knowledge.

The lack of certainty or confidence is called uncertainty.

Edit

8 Epistemic vs. aleatory uncertainty

Epistemic uncertainty arises because of the lack of our knowledge.

Aleatory uncertainty arises because of randomness.

Edit

9 Probability distribution

A probability distribution represents the frequency or probability of occurrence of different values of a random variable.

A random variable is described by its probability distribution.

Statisticians and probabilists love normal distributions thanks to the central limit theorem.

\[f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\] where

$x$ is a random variable,
$\mu$ is the mean or expected value of $x$, and
$\sigma$ is the standard deviation.

Edit

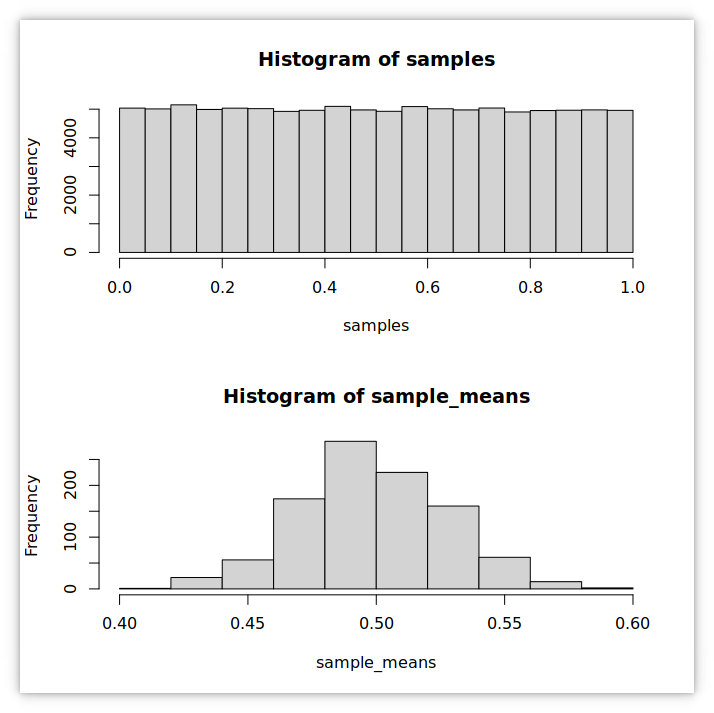
10 Central limit theorem demo

# R code by Huidae Cho
samples <- c()
sample_means <- c()
for(i in 1:1000){
  sample <- runif(100)                          # take 100 random values from a uniform distribution
  samples <- c(samples, sample)                 # collect samples
  sample_means <- c(sample_means, mean(sample)) # collect sample means
}
par(mfcol=c(2,1))
hist(samples)                                   # plot the histogram of samples
hist(sample_means)                              # plot the histogram of sample means

Edit

11 Statistics

Descriptive statistics is used to describe data. Examples?

Mean $\mu=\frac{\sum_{i=1}^n x_i}{n}$
Variance $\sigma^2=\frac{\sum_{i=1}^n(x_i-\mu)^2}{n}$

Inferential statistics is used to make predictions. Examples?

Hypothesis tests
Regression analysis

Edit

12 Reading materials

Edit